Las Matemáticas del Machine Learning: Ejemplos de Regresión Lineal (II) y Multilineal

25 de abril de 2019
En el anterior artículo vimos el concepto de recta de Regresión Lineal , y cómo obtener sus parámetros o coeficientes estadísticos. Vamos a ver ahora un ejemplo práctico donde podemos aplicarla.

1. Regresión lineal: La siguiente tabla muestra el índice de mortalidad (Y) y el consumo medio diario de cigarrillos (X) para poblaciones distintas: Figura 1: tabla de datos mortalidad por consumo tabaco. Figura 1: tabla de datos mortalidad por consumo tabaco.
¿Qué índice de mortalidad se podría predecir para una población que consume una media de 32 cigarrillos diarios?
Buscamos nuestra expresión, Y=b0 + b1X, para ello necesitaremos calcular b0 y b1, para calcular nuestros coeficientes estadísticos obtendremos las medias, varianzas y covarianzas muestrales:
Medias, varianzas y covarianzas muestrales. Figura 2: Medias, varianzas y covarianzas muestrales.

Por lo tanto, nuestra recta de regresión queda determinada por la siguiente ecuación:

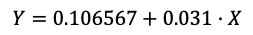Ecuación de la recta de regresión. Figura 3: Ecuación de la recta de regresión.

Veamos el coeficiente de correlación, para determinar la “proximidad” de nuestra recta:

Coeficiente de correlación. Figura 4: Coeficiente de correlación.

Es un valor muy próximo a 1, por lo que la dependencia de las variables es muy directa:

A mayor consumo medio diario de cigarrillos diarios, mayor índice de mortalidad.

Por último calculemos el índice mortal de nuestra población:

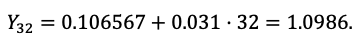Índice de mortalidad. Figura 5: Índice de mortalidad. 2. Regresión Multilineal:

Hasta ahora hemos considerado el método lineal, es decir, una variable dependiente y otra independiente, pero ¿qué pasaría si encontramos que una variable depende de más de una variable? Pues bien, cuando tenemos una extensión del modelo lineal, es decir, cuando tenemos más de una variable independiente o explicativa, estaremos hablando del modelo de Regresión Lineal Múltiple, o Multilineal.

Nuestro modelo sigue de la siguiente relación entre las variables explicativas o independientes (x1,x2,x3,…xn) y la variable respuesta o dependiente (y):

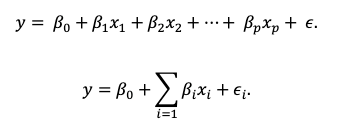Fórmula de regresión multivariable. Figura 6: Fórmula de regresión multivariable.

Donde ϵi, sigue una distribución Normal N(0 , σ^2 ), es el error de observación, β0 es el término independiente. Es el valor esperado de y cuando x1,…,xp son cero, βi mide el cambio en y por cada cambio unitario en xi, manteniendo el resto de variables constantes.

¿Qué información muestral tenemos?

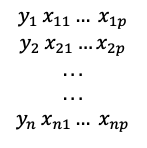Figura 7: Información muestral. Figura 7: Información muestral.

Por lo que el valor que el modelo estimado predice para la observación i-ésima es:

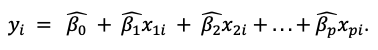Figura 8: Valor estimado para la observación i-ésima.

Y el error cometido en nuestra predicción será:

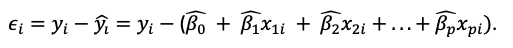Error en la predicción. Figura 9: Error en la predicción. Donde: 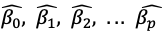Valores estimados. Figura 10: Valores estimados.

nos muestra los valores estimados del modelo. El criterio de mínimos cuadrados asignado valores a nuestros valores estimados, tales que minimiza el valor de la suma de los errores al cuadrado de las observaciones.

Podemos plantear el modelo en forma matricial de la siguiente forma:

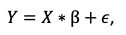Ecuación matricial. Figura 11: Ecuación matricial.

o bien:

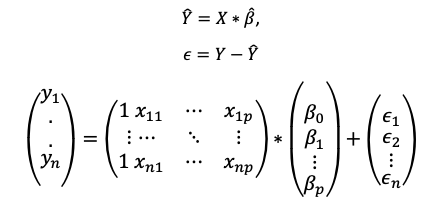Ecuación matricial extendida. Figura 12: Ecuación matricial extendida.

Para estimar el vector de parámetros β, aplicaremos el método de mínimos cuadrados de manera análoga al modelo lineal simple. El criterio de mínimos cuadrados asigna a los parámetros del modelo el valor que minimiza la suma de errores al cuadrado de todas las observaciones. Así pues sea S la suma de los errores al cuadrado:

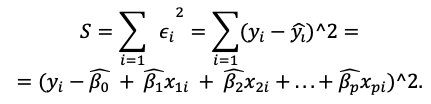Ecuación cálculo suma errores cuadrados. Figua 13: Ecuación cálculo suma errores cuadrados.

Para calcular el mínimo de S, lo que hacemos es primero derivar S con respecto a los parámetros, luego igualar a cero cada derivada (quedándonos un sistema de ecuaciones en el que cada incógnita viene dada por los parámetros que queremos estimar), y por último resolver el sistema de ecuaciones.

En términos matriciales:

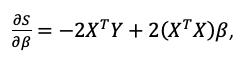Cálculo de la derivada de S respecto a los parámetros. Figura 14: Cálculo de la derivada de S respecto a los parámetros.

Siendo X^T la matriz traspuesta e igualando a 0 obtenemos:

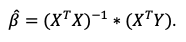Valores de los parámetros que minimizan S. Figura 14: Valores de los parámetros que minimizan S.

Ejemplo:

Veamos a continuación un ejemplo de un estudio sobre la abundancia (Recuento) de un parásito en 15 localizaciones diferentes en función de su temperatura y la humedad. Los datos obtenidos son los siguientes:

Tabla de datos sobre presencia de un parásito según CC temperatura/humedad. Figura 15: Tabla de datos sobre presencia de un parásito según CC temperatura/humedad. 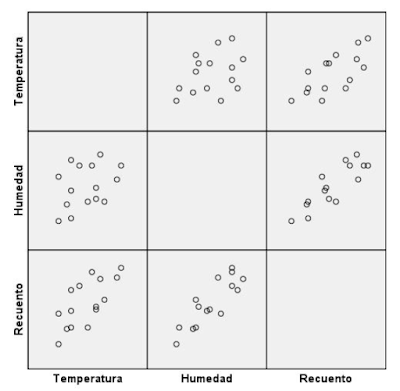Representación gráfica de la tabla anterior. Figura 16: Representación gráfica de la tabla anterior.

Al parecer tanto la temperatura como la humedad influyen en el recuento:

Aplicación de la fórmula de regresión multilineal. Figura 17: Aplicación de la fórmula de regresión multilineal.

Sean:

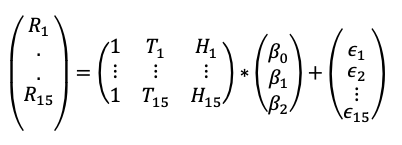Figura 18: Expresión matricial.

Si aplicamos los cálculos anteriores obtenemos:

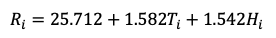Valores obtenidos. Figura 19: Valores obtenidos.

En el siguiente artículo, veremos qué conclusiones obtenemos a partir de la muestra, así como la coolinealidad de las variables independientes y cómo estas pueden afectar a nuestro modelo. Por último hablaremos de los contrastes de hipótesis y de los intervalos de confianza.

Esto es todo por hoy ;), hasta el próximo capítulo de nuestra serie de las Matemáticas del Machine Learning. Cualquier duda podéis publicarla como comentario en este mismo artículo.

No te pierdas los artículos anteriores:

Escrito por Fran Fenoll (@ffenoll16), Fran Ramírez (@cyberhadesblog y @cybercaronte) y Enrique Blanco (@eblanco_h) ambos del equipo de Ideas Locas CDO de Telefónica.