Colisiones, haberlas hay(las). Parte 3.

24 de mayo de 2018
En la entrada anterior sobre este tema comentamos la idoneidad del algoritmo ECDSA y más concretamente, de la curva “secp256k1”. No estando afectado por vulnerabilidades conocidas, se podría considerar seguro, aunque esto, depende en gran medida de cómo se utilice. Pues, ¡vamos a analizarlo!

Claves privadas de Bitcoin
Al igual que otros sistemas de Criptografía Asimétrica, ECDSA se fundamenta en el binomio de claves privadas y claves públicas. En Bitcoin, según están definidos los parámetros de dominio de la curva “ secp256k1”, una clave privada puede ser cualquier número comprendido entre 1 y el número de puntos de la curva u orden “n” menos 1:

n = 115792089237316195423570985008687907852837564279074904382605163141518161494337 - 1

El valor de “ n-1” es algo menos de 2^256, pero es un número tremendamente grande. Tanto, que cuesta trabajo imaginarse sus colosales dimensiones, e incluso escribirlo en formato decimal, ya que tiene 78 cifras, aproximadamente 10^77.

10^77 es un número tan descomunal, que es difícil incluso de comparar; los granos de arena de todas las playas del planeta rondan los 10^20, y todas las estrellas del Universo apenas llegan a 10^23. Solo el cálculo aproximado de todos los átomos del Universo 10^80, está en su orden de magnitud, siendo ambos sobrepasados ampliamente por el Número de Shannon 10^120, que representa el número teórico de partidas de ajedrez posibles.

Mientras que no se descubra alguna vulnerabilidad en el algoritmo, o la computación cuántica consiga llevar la capacidad de computo a limites desconocidos, se puede considerar que una clave privada de 256 bits es suficientemente segura para criptosistemas de curva elíptica, siempre y cuando dicha clave sea generada de forma verdaderamente aleatoria.

Si la generación de la clave privada se lleva a cabo de forma verdaderamente aleatoria, la probabilidad de colisión tiende tanto a cero que no puede, ni siquiera, llegar a tenerse en consideración.

Existen precedentes donde una implementación errónea de la generación de claves, o como parte de alguna prueba de concepto, se utiliza un número, no ya predecible, sino simplemente igual a “1” (primera clave privada) o igual a “n-1” (última clave privada) como clave privada.

Matemáticamente es posible resolver la ecuación de la curva con un número de clave privada mayor a “n-1”, por ejemplo “n”, pero al tratarse de un factor modular, el resultado será la misma clave pública generada a partir de la clave privada “1”. Esto no puede considerarse una colisión de claves privadas; la mayoría de las implementaciones devuelve un error al tratar de utilizar como clave privada un valor superior a “n-1”. Por ejemplo en el módulo pybitcoin de Python v2.7:

raise IndexError(_errors["EXPONENT_OUTSIDE_CURVE_ORDER"]) IndexError: Secret exponent is outside of the valid range. Must be >= 1 and < the curve order.

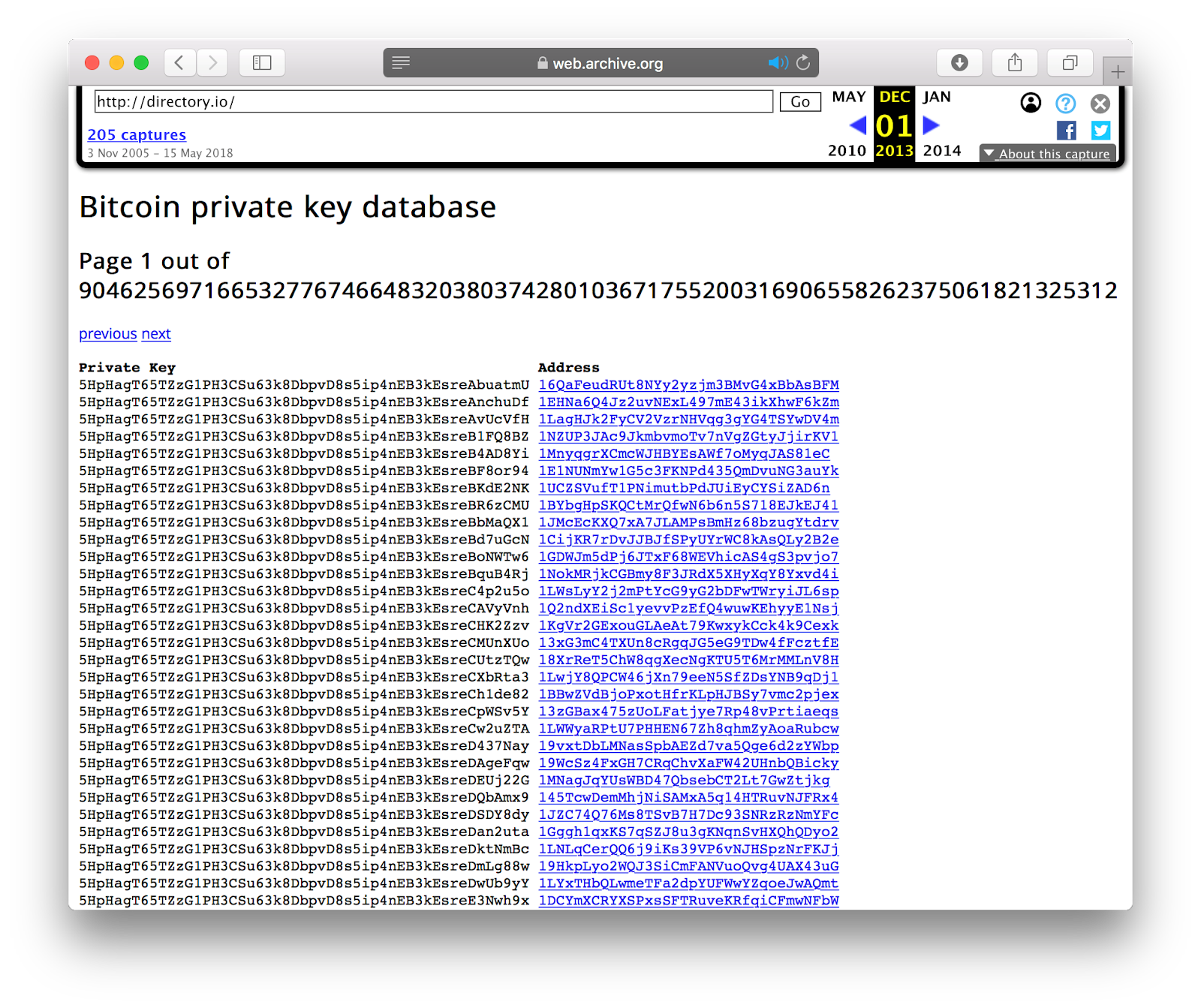
En cualquier caso, ya sea por error, como parte de una prueba de concepto, o por mera experimentación, las direcciones de Bitcoin correspondientes a las claves privadas “1” y “n-1”, han sido utilizadas en el pasado, y sorprendentemente, continúan siendo utilizadas en el presente, tal y como se puede comprobar explorando la cadena de bloques:

¿Quiere esto decir que se conocen las claves privadas de todas las direcciones de Bitcoin? No, más bien, lo que quiere decir es que, se pueden calcular las direcciones de Bitcoin de todas las claves privadas que existen; el problema es, como hemos visto, que son demasiadas.

Son tantas que, en base a la potencia de cálculo actual, se tardarían decenas de miles de millones años en computarse; sin mencionar que, un hipotético dispositivo para almacenarlas excedería el tamaño de nuestra galaxia.

No obstante, estos pequeños detalles no han supuesto un impedimento a la hora de tratar de representar todas las claves privadas y sus direcciones de Bitcoin correspondientes. Sí, “todas”, pero no de golpe, solo aquellas que se consulten. Este fue precisamente el objetivo del proyecto directory.io, el cual hoy ya no está operativo, pero han surgido otras muchas webs, donde con algo de publicidad, ofrecen un servicio similar e incluso mejorado, al consultar en la cadena de bloques los fondos que pudiera haber en las direcciones de Bitcoin obtenidas:
En la siguiente captura del 1 de diciembre de 2013 almacenada por archive.org, se observa como directory.io muestra únicamente las direcciones sin comprimir, que eran las más utilizadas en los primeros años de Bitcoin, destacando que comienza por la polémica dirección no valida “ 16QaFeudRUt8NYy2yzjm3BMvG4xBbAsBFM”, ya que, pese a haber recibido varias transacciones, no es una dirección utilizable, al corresponderse con una clave inexistente, cuyo valor teórico sería cero. Su jocosa FAQ estaba repleta se sarcasmos.

El código fuente original de directory.io estuvo disponible por algún tiempo, y pese a que no aportaba ninguna novedad destacable, ciertos matices en su estructura eran semejantes a los encontrados en el código fuente original de Bitcoin que publicó Satoshi Nakamoto. Por ello, se vinculó al creador de Bitcon con su mantenedor, Arran Walker, que además publica en su espacio de GitHub una variante optimizada en lenguaje GO.

captura de pantalla almaceada por archive.org imagen
No es necesario mencionar que cualquier cantidad de bitcoins transferida a cualquiera de estas direcciones cuya clave privada es conocida, es inmediatamente sustraída por alguno de los cientos de “ bots” que están monitorizando permanentemente el “mempool” de la red de Bitcoin, a la espera de una transacción incauta.

Esta operativa de robo de bitcoins de forma automática e instantánea por medio de bots, que incluso compiten entre ellos, fue diseccionada por Yaiza Rubio y Felix Frezo en la ponencia que ofrecieron en la RootedCON de 2015. El objetivo en esta ocasión eran las direcciones de Bitcoin generadas a partir de “ carteras mentales”; una práctica totalmente desaconsejada, ya que los bots cuentan con millones de claves precalculadas, a partir de diccionarios de múltiples idiomas y de contraseñas habituales. Este uso ha sido relegado a favor del BIP0039, que genera una estructura de claves y direcciones de modo determinista a partir de una relación de 12 palabras a elegir entre 2048, con la que se obtiene una entropía de 128 bits; de momento suficiente para mantener a salvo cualquier wallet.

De igual forma que no se puede considerar una colisión de clave privada cuando esta ha sido generada sin la suficiente aleatoriedad, tampoco se puede considerar una colisión cuando la clave privada ha sido generada a partir de una contraseña o palabras de un diccionario conocido o susceptible de haber sido previamente calculado.

Se deduce entonces, que no existen colisiones conocidas, ni riesgo de haberlas a corto plazo, en las claves privadas de Bitcoin, siempre que estas se generen con suficiente aleatoriedad. Pero, ¿qué ocurre con las claves públicas y sobre todo con los algoritmos de hash SHA-256 y RIPEMD-160?, ¿serán suficientemente seguros para impedir colisiones en las direcciones de Bitcoin?

Te lo contaremos todo en la cuarta parte, ¡no te pierdas la próxima entrega hacker! Y recuerda que si tienes dudas o quieres discutir más sobre el tema, puedes visitarnos en la Comunidad de ElevenPaths.

Jorge Rivera
CSA, Chief Security Ambassador
» Colisiones, haberlas hay(las). Parte 1
» Colisiones, haberlas hay(las). Parte 2
» Colisiones, haberlas hay(las). Parte 4