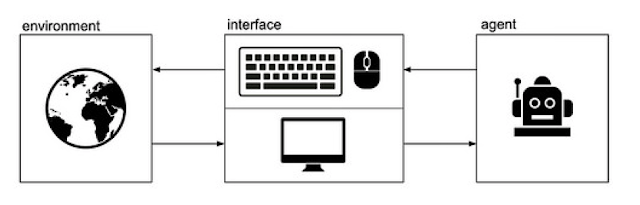
El siguiente paso será inicializar las variables. Aquí utilizaremos la primera función de
, la cual simplemente rellena de ceros una matriz bidimensional donde utilizamos los valores de
= 6, son el número de acciones que podemos realizar La matriz tendría por ejemplo, una estructura similar a esta:
indicará la media de aprendizaje y es un valor entre 0 y 1. Si el valor es 0, no habrá aprendizaje, los
(valores Q de la tabla en cada celda) no se actualizarán y si el número es alto, como por ejemplo 0.9 ocurrirá más rápido pero actualizará menos los valores de las tablas, siendo menos preciso. Lo dejaremos en un valor de 0.2.
Antes de explicar la siguiente parte del código que incluye la función
run_episode, vamos a ver primero la parte principal de ejecución, de esta forma entenderemos mejor luego el funcionamiento de dicha función. Observamos el bucle que ejecutará los episodios, en nuestro caso hemos definido 2000:
for episode in range (0,2000):
Luego inicializamos las variables que vamos a utilizar en cada ejecución de episodio, entre ellas también el entorno con la variable
observation y
env.reset()
out_done=None
reward = 0
rewardstore=0
observation = env.reset()
A continuación, tenemos un bucle tipo
while que se ejecutará siempre y cuando la variable
out_done no sea igual a
True. Este bucle ejecuta todas las acciones que hemos definido y que veremos más adelante, hasta que el episodio termine (resolviendo o no el episodio) devolviendo el valor
True a dicha variable.
En la variable
action almacenaremos la acción que vamos a realizar en cada paso de la resolución de los episodios. En este caso, seleccionamos con la función
np.argmax el índice o la posición de las 5 que acciones que tenemos donde se encuentra el valor máximo. Por ejemplo, supongamos que tenemos la siguente salida
Q en el estado 64, podemos ver los valores de la matriz
Q[64] con los valores
[ -0.2, -0.2 , -0.2, -0.2, -2, 0 ] equivalentes a una lista de 6 elementos:
Al ser una lista, la ejecución de
np.argmax nos devolverá un número con la
posición índice donde se encuentra el valor máximo, en este caso, posición numero 6 (0 al 5) que contiene el valor 0 y que a su vez corresponde con la acción de recoger al pasajero (
Pickup).
action = np.argmax(Q[observation])
La siguiente parte del código llama la función
run_episode utilizando como parámetros la variable
observation y
action. Esta función devolverá tres valores:
- out_done: ya la hemos comentado antes, devolverá True cuando termine el episodio
- out_totalreward: devolverá un número entero con la recompensa obtenida
- out_observation: devolverá un número entre 0 y 500 que nos indicará en qué estados están las variables del entorno después de realizar una acción (por ejemplo, la nueva ubicación del taxi o si hemos recogido o no un pasajero)
out_done, out_totalreward, out_observation = run_episode(observation,action)
La recompensa obtenida en la ejecución de estas acciones la acumularemos en la variable
rewardstore (para tener un valor global de recompensa) y actualizamos los valores de la nueva observación recibida desde
out_observation almacenándolos en la variable
observation para preparar la siguiente ejecución de acciones:
rewardstore += out_totalreward
observation = out_observation
Finalmente, visualizamos al finalizar cada episodio, los valores totales obtenidos como recompensa:
print('Episodio {} Recompensa: {}'.format(episode,rewardstore))
Ahora pasamos a analizar la función
run_episode, donde se realizan todas las operaciones importantes del algoritmo. Esta función recibe como parámetros la observación actual (recordemos, un valor entre 0 y 500 que corresponde a la situación actual de los estados del entorno, variable
observation1) y el movimiento que vamos a realizar con nuestro taxi (variable
movimiento):
def run_episode(observation1, movimiento):
La primera acción a realizar será ejecutar los movimientos que hemos recibido como parámetros. Para ello utilizamos la función
env.step(movimiento). Esta ejecución devolverá 4 valores:
- observation2: situación en la que queda el entorno después de nuestro movimiento
- reward: recompensa obtenida
- done: si hemos finalizado
- info: datos estadísticos (que no usaremos de momento)
observation2, reward, done, info = env.step(movimiento)
Una vez recibida toda esa información procedemos a actualizar la tabla
Q con los valores obtenidos después de utilizar la fórmula que explicamos en el anterior artículo:
Y que se traduce en código
Python de la siguiente manera:
Q[observation1,movimiento] += alpha * (reward + np.max(Q[observation2]) - Q[observation1,movimiento])
Básicamente, lo que está ocurriendo durante la ejecución de esta función y del algoritmo, es lo siguiente. Como ya hemos comentado, la tabla
Q es una matriz
NxM, donde
N es el número de estados y
M las acciones a realizar (definido por las variables
env.observation_space.n y
env.action_space.n respectivamente). En función de estado donde nos encontremos (en el caso de la imagen anterior era el 64), se comprueba la fila (que básicamente es una lista, como se puede ver también en la imagen) y cada columna (acción) lo que vamos almacenando o comprobando es la probabilidad de elegir esa acción. Así poco a poco vamos construuendo nuestra tabla
Q con los valores más óptimos posibles. En el último paso la función devuelve los valores
done, reward y
observation2 (los cuales corresponderán a las variables
out_done, out_totalreward y
out_observation:
return done,reward, observation2
Finalmente obtendremos una matriz
Q rellena con los valores óptimos para cada posible estado que pueda ofrecer este entorno. La visualización de los algoritmos, datos y tiempos de aprendizaje (ejecución) son muy importantes, por eso vamos a ver cómo crearlos. En este caso, vamos a utilizar la librería
Matplotlib para
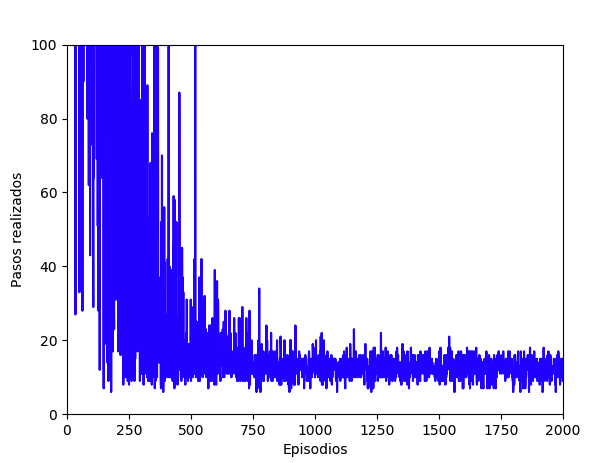
Python para dibujar dos gráficas, la primera de ellas mostrará la evolución de los pasos necesarios a ejecutar en cada episodio hasta encontrar una solución óptima al problema. Por otro lado, también mostraremos la evolución de las recompensas obtenidas. Este primer gráfico muestra como a medida que avanzan los episodios de entrenamiento, son necesarias menos ejecuciones de pasos para encontrar la solución óptima. De hecho, a partir de más o menos los 600 episodios ya podemos notar la disminución del número de pasos a ejecutar:
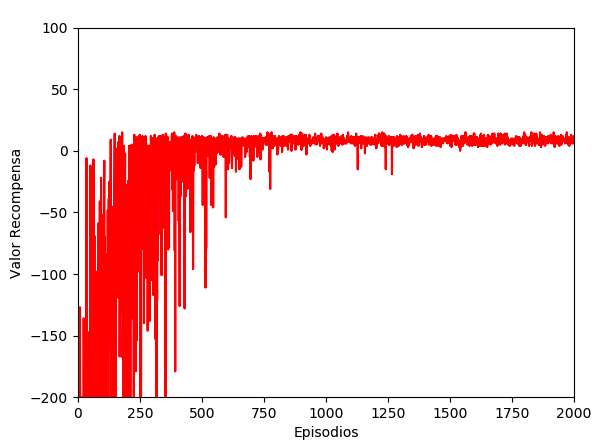
Y este otro gráfico muestra el valor de las recompensas, siendo las primeras valores negativos hasta su normalización en valores positivos. De nuevo, más o menos sobre el episodio 600 es cuando comienza a estabilizarse la obtención de recompensas positivas:
Crear estos gráficos es sencillo, simplemente instalamos la librería
Matplotlib en nuestro entorno Linux:
sudo apt-get install python3-matplotlib
Luego la importamos dentro del código:
import matplotlib.pyplot as plt
Y finalmente dibujamos un eje de coordenadas
x e
y con rango x desde 0 a 2000 (número de episodios) y como rango y desde 0 a 100 (pasos máximos por episodio). Luego etiquetamos los ejes con el comando
plt.xlabel y
plt.ylabel y finalmente lo dibujamos con el comando
plt.plot. La variable
episodios será una lista de elementos con los valores de 1 a 2000 y la variable
pasostotal será una lista con el número de pasos ejecutados por cada episodio. Por otro lado, la variable
recompensas será también una lista donde almacenamos la recompensa obtenida en cada episodio:
#Gráfica de pasos por episodio
plt.axis([0,2000,0,100])
plt.xlabel('Episodios')
plt.ylabel('Pasos realizados')
plt.plot(episodios,pasostotal,color='blue')
plt.show()
#Gráfica de recompensa por episodio
plt.axis([0,2000,-200,100])
plt.xlabel('Episodios')
plt.ylabel('Valor Recompensa')
plt.plot(episodios,recompensas,color='red')
plt.show() A continuación mostramos un vídeo con la ejecución y el código fuente final el cual es una modificación del principal que aparece al principio de este artículo, pero esta vez se muestra una ejecución paso a paso, donde vemos todos los valores de la tabla
Q así como una visualización de los estados (simulando una animación). Al final de proceso, el cual será largo ya que son 2000 episodios se mostrarán los gráficos. Para acelerarlo podemos comentar todos los comandos
print que no necesitemos y sobre todo la la línea
input(“->”), la cual espera que pulsemos una tecla para continuar con la ejecución. En el siguiente video podemos ver este proceso, tanto la salida de ejecución como la modificación de los comandos:
import gym
import numpy as np
import matplotlib.pyplot as plt
env = gym.make("Taxi-v2")
#Inicializacion de variables
Q=np.zeros([env.observation_space.n, env.action_space.n])
pasos=0
alpha=0.2
episodios=[]
pasostotal=[]
recompensas=[]
def run_episode(observation1, movimiento):
observation2, reward, done, info = env.step(movimiento)
Q[observation1,movimiento] += alpha * (reward + np.max(Q[observation2]) - Q[observation1,movimiento])
return done,reward, observation2
for episode in range (0,2000):
episodios.append(episode)
pasos=0
out_done=None
reward = 0
rewardstore=0
observation = env.reset()
print("OBSERVACION: ",observation)
print("Estado inicial:")
print(env.render()) # muestra estado inicial
while out_done != True:
pasos+=1
action = np.argmax(Q[observation])
print("Estado ",observation,"valor matriz Q: ",Q[observation])
print("Valor máximo en posición ",action+1," de la lista")
print("Acción: ",action)
print(env.render())
input("->")
print(chr(27) + "[2J") #Borra pantalla
out_done, out_totalreward, out_observation = run_episode(observation,action)
rewardstore += out_totalreward
observation = out_observation
recompensas.append(rewardstore)
pasostotal.append(pasos)
print("Estado final:")
print(env.render()) # muestra estado final
print('Episodio ',episode,' Recompensa: ',rewardstore)
#Gráfica de pasos por episodio
plt.axis([0,2000,0,100])
plt.xlabel('Episodios')
plt.ylabel('Pasos realizados')
plt.plot(episodios,pasostotal,color='blue')
plt.show()
#Gráfica de recompensa por episodio
plt.axis([0,2000,-200,100])
plt.xlabel('Episodios')
plt.ylabel('Valor Recompensa')
plt.plot(episodios,recompensas,color='red')
plt.show()
Las
tablas Q son un recurso de
Machine Learning relativamente fácil de utilizar con resultados muy buenos en entornos con pocos estados. En nuestro caso jugando con
Taxi tenemos 500 estados, fáciles de calcular, el problema llega cuando queremos enseñar a nuestra
IA a jugar en entornos más complejos como
PacMan o
Doom los cuales tienen infinitos estados para procesar. En estos casos es imposible utilizar las
tablas Q pero sí podemos utilizar las
DQN cuya base es
Q-Learning y también tendremos que utilizar el análisis de imágenes, fotogramas de la ejecución del juego e interpretarlos. Esto es lo que veremos en nuestro próximo artículo que posiblemente será otra serie, no te la pierdas, esto era divertido pero ahora empieza lo mejor ;)
Artículos anteriores:
 Cloud Híbrida
Cloud Híbrida Ciberseguridad & NaaS
Ciberseguridad & NaaS AI & Data
AI & Data IoT y Conectividad
IoT y Conectividad Business Applications
Business Applications Intelligent Workplace
Intelligent Workplace Consultoría y Servicios Profesionales
Consultoría y Servicios Profesionales Pequeña y Mediana Empresa
Pequeña y Mediana Empresa Sanidad y Social
Sanidad y Social Industria
Industria Retail
Retail Turismo y Ocio
Turismo y Ocio Transporte y Logística
Transporte y Logística Energía y Utilities
Energía y Utilities Banca y Finanzas
Banca y Finanzas Ciudades Inteligentes
Ciudades Inteligentes Sector Público
Sector Público