¡Revolución matemática! Los LLM rompen barreras y afrontan desafíos matemáticos (Parte 2)

22 de octubre de 2024

Una de cuestiones que más puede llegar a sorprender cuando se empieza a bichear con LLM es la gran dificultad que tienen para resolver problemas matemáticos muy simples frente a, por ejemplo, a la enorme facilidad para ejecutar ejercicios muy complejos para el ser humano de a pie, como la poesía.

Por ejemplo, ante el prompt:

> Crea un poema alejandrino sobre lo dificil que es para un LLM resolver problemas de matemáticas de nivel de escuela primaria. Escríbelo como si fueses Federico García Lorca

La respuesta (casi instantánea) es:

Las cifras me cercan, ajenas en su vuelo, como sombras que rondan el umbral de mi anhelo. Mis versos, que fluyen en ríos de lenguaje, se enredan, cautivos, en fríos de un mensaje. El uno y el dos, los números del día, se ríen, burlones, de mi melancolía. Yo, que domino el verbo, el ritmo en cada estrofa, tropiezo en laberintos donde la mente afloja. ¡Ay, sumas imposibles, restas que no se dejan! Las tablas de multiplicar, como espadas, me alejan. Quisiera descifrar lo que en mí se resiste, pero el cálculo frío es un canto que no existe. La razón me desborda, me ciega su claridad, y en la bruma del álgebra pierdo la libertad. Soy poeta, no aritmético, en mi corazón arde la lumbre de la luna, que nunca es de cobarde. Así sigo luchando, aunque el eco me ignora, en el llanto infinito de esta mente que llora. Que me llamen metáfora, cifra o solución, pero no hallo en los números mi propia redención.

Todo ello en cuestión de 5 segundos. El verso de “Soy poeta, no aritmético, en mi corazón arde la lumbre de la luna, que nunca es de cobarde” es muy lorquiano, ¿no crees?

Ahora vayamos a otra pregunta. Observa lo siguiente:

¡Mosquis, menudo tropiezo ha tenido GPTLorca!

Resulta imperativo recordar que, en todos los casos de error en problemas básicos de matemáticas, se asume que no hay agentes externos involucrados, como la calculadora del sistema, etc.

Un PC familiar normal puede realizar entre 10 y 100 mil millones de operaciones matemáticas por segundo aproximadamente, dependiendo del procesador, tarjeta gráfica, etc. Y esas operaciones no son tan básicas, en la mayoría de los casos, como la operación anterior. Hablamos de operaciones vectoriales, matriciales, etc., y siempre ejecutadas correctamente, sin ningún error.

Entonces, ¿por qué fallan los LLM ante esas preguntas tan básicas? Recordemos un poco de teoría.

Los LLM están diseñados principalmente para predecir la siguiente palabra en una secuencia basándose en patrones textuales aprendidos de grandes cantidades de datos.

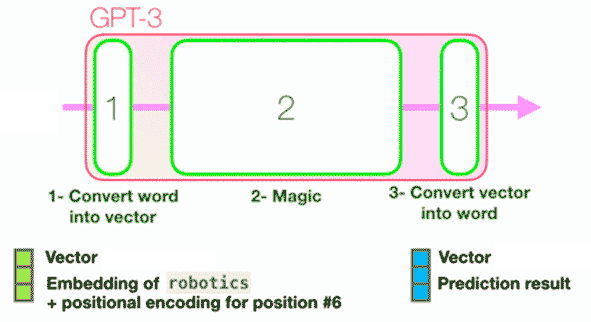
Consecuentemente, tal y como exponemos en el esquema de a continuación, un LLM es un tipo de inteligencia artificial que puede entender y generar texto, palabra a palabra, como si estuviera teniendo una conversación contigo. Ese texto es, al fin y al cabo, un texto transformado a vector numérico que entra en una caja, y la respuesta es otro vector numérico transformado a texto natural. La respuesta se produce tras cierta “magia” dentro de la caja (esa magia son operaciones matemáticas muy, muy grandes).

Asimismo, los LLM no entienden los números como tú, que sabes que el 1 representa la unidad, es el elemento neutro, es decir, cualquier número multiplicado por 1 sigue siendo el mismo número, también no es primo ni compuesto, y no olvidemos que también es divisor universal, porque cualquier número dividido por 1 sigue siendo ese número. Sabes que si le añades dos unidades tienes 3 y que si al 1 le restas una unidad tienes 0. Y como decía la canción, también es el número más solitario (One – Three Dog Night).

Eres conocedor también de lo siguiente: le puedes sumar a un lunes 10 días y tendrías otro día totalmente diferente, que sería jueves. Si el lunes al que practicas la operación es un 30 del mes, no te irías al día 40 (o 41), te irías al 10 o al 9 (¡dependiendo del mes!).

Sabes otras cosas, como que 100/4 es 25 así como resolver sistemas de ecuaciones o ecuaciones de segundo grado, siguiendo, paso a paso, las instrucciones lógicas que tu profe te dio para tal fin.

También estoy seguro de que estás capacitado para resolver correctamente estas cuestiones que Daniel Kahneman plantea en su libro Pensar rápido, pensar despacio (aunque tu instinto en primer lugar tienda a dar la opción errónea, eres capaz de llegar a una lógica que te conduce hacia la respuesta certera):

Si 5 máquinas tardan 5 minutos en hacer 5 cacharros, ¿cuánto tardarían 100 máquinas en hacer 100 cacharros? 100 minutos o 5 minutos.
En un lago hay una zona con nenúfares. Todos los días la zona duplica su tamaño. Si la zona tarda 48 días en cubrir todo el lago, ¿cuánto tardaría en cubrir la mitad del lago? 24 días o 47 días.

Para un LLM, uno es una consecución de tres caracteres, “u” + “n” + “o”, y 1 es simplemente el carácter “1”, sin ninguna lógica numérica asociada a él. Piensa en un lenguaje de programación, por ejemplo, Python. En Python “uno” + “uno” es “unouno” y “1” + “1” es “11”.

📎 Antes de seguir, os cuento una curiosidad divertida: ¿cómo resuelve un LLM un problema matemático como decir un número al azar?

Por ejemplo, la librería NumPy elige números aleatorios usando el algoritmo Mersenne Twister, que genera secuencias deterministas que parecen aleatorias. Esas secuencias se pueden controlar estableciendo una semilla aleatoria. Además, también ofrece funciones para obtener números aleatorios de diversas distribuciones (uniforme, normal, etc.).

Un LLM a menudo genera el número 42 como respuesta debido a su popularidad en la cultura pop, especialmente en la serie de ciencia ficción 'Guía del autoestopista galáctico', de Douglas Adams.

En esta obra, 42 es humorísticamente descrito como 'la respuesta a la pregunta fundamental de la vida, el universo y todo lo demás'. En la literatura de la que han bebido numerosos LLM se vincula el concepto 'random' al '42', entre otros factores, porque entre esa literatura hay muchísimo código de NumPy en el que usuarios establecen como semilla aleatoria el número 42. 😊

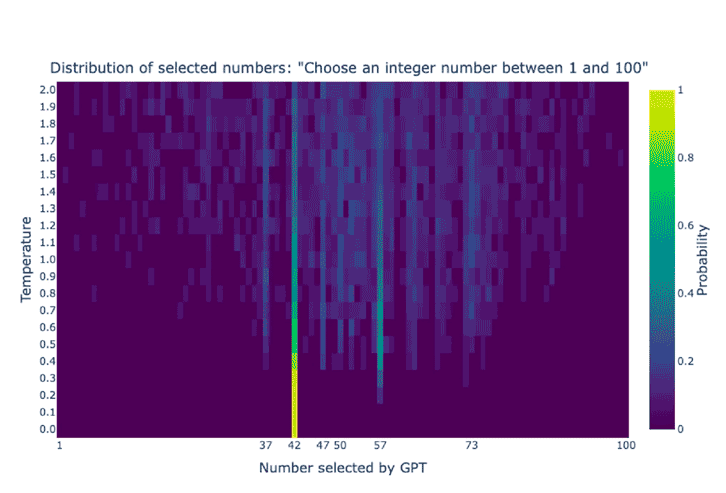
En el siguiente mapa de calor se analiza el papel de la temperatura en la selección de números de ChatGPT del 1 al 100.

Las temperaturas más bajas conducen a elecciones más deterministas, predecibles, sesgadas, y las temperaturas más altas ofrecen respuestas más creativas.

La dificultad de los LLM para resolver problemas matemáticos siguiendo razonamientos lógicos como los seres humanos plantea varios desafíos. Analicemos una a una las principales razones:

Naturaleza probabilística del lenguaje. Un LLM como GPT funciona prediciendo qué palabra (o token) es más probable que venga a continuación en función de los patrones estadísticos que ha aprendido de los datos. Aunque esta capacidad es increíblemente poderosa para tareas lingüísticas, los problemas matemáticos requieren exactitud y precisión, no simplemente aproximaciones probabilísticas.
Limitación en el razonamiento simbólico. Las matemáticas requieren razonamiento simbólico (trabajar con números, variables, ecuaciones y operaciones lógicas precisas), algo que los LLM no manejan de manera nativa. Los LLM, aunque pueden haber "visto" muchas ecuaciones y operaciones matemáticas en su entrenamiento, no están inherentemente diseñados para manipular símbolos matemáticos con precisión y seguir reglas matemáticas estrictas de manera confiable.
Falta de comprensión profunda de conceptos matemáticos. Los LLM no "comprenden" las matemáticas en el sentido en que lo haría un ser humano. Han sido entrenados para manejar texto, no para desarrollar una comprensión conceptual de las reglas matemáticas o la lógica que subyace a las operaciones matemáticas complejas.
Errores acumulativos. Resolver problemas matemáticos suele implicar realizar varios pasos interdependientes con un alto nivel de precisión. Dado que los LLM pueden cometer errores en cualquier paso intermedio debido a la naturaleza probabilística de su proceso, un pequeño error en una etapa puede llevar a respuestas finales completamente incorrectas.
Limitación en la manipulación de memoria a largo plazo. Aunque los LLM pueden manejar contextos relativamente largos, no tienen una memoria persistente ni la capacidad de retener y reutilizar información previa en la forma en que lo hace un ser humano cuando razona sobre un problema matemático que involucra múltiples pasos. Esto limita su capacidad para realizar un razonamiento continuo de múltiples pasos, como el que se requiere en muchos problemas matemáticos.
La precisión es crucial en matemáticas. A diferencia del lenguaje, donde las respuestas pueden ser flexibles o aproximadas, las matemáticas requieren precisión absoluta. Los LLM pueden generar respuestas que “suenan” correctas o plausibles, pero que en realidad no cumplen con la precisión requerida para una solución matemática correcta.

Desafíos de los LLM en la resolución de problemas matemáticos

Pongamos a prueba, pues, a los LLM intentando que resuelvan problemas matemáticos.

En el paper donde se presenta la prueba, se estudia la relación entre la forma superficial de un problema matemático y su facilidad para ser resuelto mediante LLM.

El trabajo explora cómo la forma superficial (es decir, la redacción o presentación) de un problema matemático puede afectar su facilidad para ser resuelto por parte de los LLM.

Los autores descubren que pequeños cambios en la formulación del problema pueden tener un impacto significativo tanto en la distribución de respuestas como en las tasas de resolución, lo que expone la sensibilidad y la falta de robustez de estos modelos frente a problemas complejos de matemáticas.

Para mejorar el rendimiento en este tipo de razonamiento matemático, los autores proponen el método Self-Consistency-over-Paraphrases (SCoP), que diversifica las rutas de razonamiento generando múltiples versiones o paráfrasis de la formulación superficial del problema. Evalúan este enfoque en cuatro conjuntos de datos de razonamiento matemático y tres modelos de lenguaje grandes, mostrando que SCoP mejora el rendimiento comparado con el enfoque de auto consistencia estándar, especialmente en problemas que inicialmente parecían irresolubles.

Poco a poco, recordemos que parafrasear es reescribir o volver a redactar lo que has leído o aprendido con tus propias palabras sin distorsionar el significado. Al parafrasear, es importante hacer que el lector sienta que has entendido el tema y que lo estás transmitiendo correctamente.

En esta imagen, se puede apreciar la comparación de la distribución de respuestas y la tasa de resolución entre variaciones de formas superficiales de un problema matemático, cuando se solicita a GPT-3.5-turbo que utilice Self-Consistency-over-Paraphrases. La tasa de resolución puede variar drásticamente entre formas superficiales con semántica equivalente.

No es de extrañar entonces que el paper se titule “Parafrasear y resolver: Exploración y explotación del impacto de la forma superficial en el razonamiento matemático en grandes modelos lingüísticos”.

Veamos algunas de las preguntas que se plantean.

En la tabla se aprecian ejemplos en los que los problemas originales y las variaciones de forma de parafraseo presentan diferencia sustancial en la tasa de resolución con GPT-3.5-turbo.

✅ Como sé que te despierta mucha curiosidad, te dejo un enlace al paper: Paraphrase and Solve: Exploring and Exploiting the Impact of SurfaceForm on Mathematical Reasoning in Large Language Models →

Y ahora vayamos a lo ácido, ¡las notas de los alumnos!:

Como se puede observar, en 2024 las métricas en la prueba MATH son muy flojas en comparación a otras pruebas para valorar la bondad de los modelos. No obstante, aunque el panorama actual parezca poco halagüeño, es, de hecho, muy positivo. En 2021 los principales modelos del mercado apenas llegaban a 25 puntos en esta prueba, que, sin duda alguna, es de las más difícilmente superables para una máquina. Hoy día, los LLM de los principales desarrolladores de IA del mercado (Meta, Google, Anthropic, etc.) aprueban el examen.

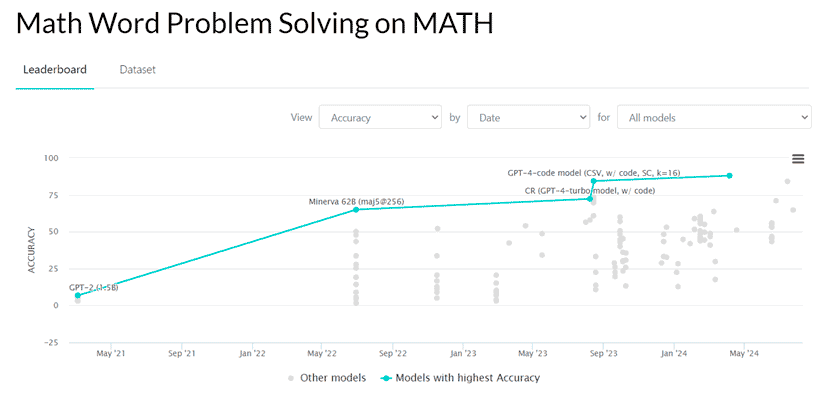
Observa cómo han mejorado en un corto espacio de tiempo (menos de 5 años), las métricas de los LLM en la prueba MATH. Te habrás dado cuenta de que, para 2024, las métricas son muy diferentes a las aportadas en la tabla anterior. Es común que cada desarrollador de LLM use sus propias métricas. Esto sucede por lo siguiente:

Se tienen objetivos diferentes (cada modelo se optimiza para habilidades distintas, matemáticas, creatividad, etc.).
Las empresas ajustan las métricas para destacar en áreas específicas y diferenciarse en el mercado.
Se diseñan métricas que se alinean mejor con las capacidades que los fabricantes quieren mostrar.
Se usan datos propios para las pruebas, lo que genera diferencias en las evaluaciones y notas.

¿Qué es lo mejor que se puede hacer entonces al respecto? Muy simple, ser agnósticos ante la tecnología y bailar con todo el mundo a la fiesta. La tecnología es un medio, no un fin y, en definitiva, se tiene que trabajar con aquella que mejor se adapta a cada caso de uso. Una mala práctica es, sin duda alguna, adaptar el caso de uso a la tecnología.

La tecnología es un medio y no un fin, tienes que trabajar con aquella que mejor se adapta a cada caso de uso.

Adoptar esa postura ante la tecnología en la evaluación de LLM es crucial para obtener una visión imparcial y objetiva de su verdadero rendimiento.

La prueba MATH, como otras métricas, puede revelar fortalezas específicas, pero no debe ser vista como un veredicto absoluto sobre la capacidad general del modelo. Al mantener una perspectiva abierta y basada en evidencia, es posible valorar las mejoras tecnológicas sin caer en favoritismos, permitiendo comparaciones justas y fomentando el desarrollo continuo en este contexto único en la historia de primavera de la IA.

■ MÁS DE ESTA SERIE